The Large Hadron Collider, buried 300 feet beneath Geneva, Switzerland and eastern France, is 27 kilometers in circumference. / Image courtesy of CERN
Editors' Note: This is the fifth article in a series on new research at CERN.
Prior to the twentieth century there was no hard distinction between experimental and theoretical physics. Some physicists (like Michael Faraday) were more talented at building things, and some (like James Clerk Maxwell) were more comfortable in the realm of pure math, but as a rule, physicists needed to be a mix of theorist and experimentalist.
Starting in the 1940s and 1950s, however, as physics became increasingly complex, the divergence between the people (like Ernest Lawrence) who built and ran the experiments and the people (like Richard Feynman) who studied the theory full time became pronounced. Enrico Fermi is perhaps the last person who could lay claim to being a leader in both areas. The training and career paths of theoretical and experimental physicists are now very different, starting from the earliest days of graduate school.
This division of labor has some large advantages. For one thing, the amount of material that must be mastered in both theory and experiment means it is no longer possible for anyone to be an expert in both areas; great work requires the collaboration of both camps.
Nevertheless physics is, like all sciences, driven by experiment. While many of the physicists who have become famous in popular culture are theorists, theory must, in the end, defer to experimental results. Even the most famous examples of triumphant, elegant theory—Einstein’s theories of special and general relativity—were responses to an experimental fact: that every measurement of the speed of light gave the same answer, regardless of frame of reference.
Theorists did not arrive at the Standard Model of particle physics because of its mathematical elegance (arguably, it is pretty kludgy, despite its symmetries). Instead, experimental physicists reported results, and the Standard Model arose as the best theoretical explanation of them. In the years between the formulation of the Standard Model and the construction of the Large Hadron Collider (LHC), we theorists have come up with many potential new stories—ideas about supersymmetry and string theories—to solve problems that the Standard Model leaves unanswered. But without data, we cannot know which of these ideas is right, if any are. (One of the most exciting things about the potential signal of new physics that kicked off this series of articles is that it cannot be easily fit into any of our pre-existing theoretical constructions.) Despite our best efforts, we cannot get by on pure thought alone.
Data about how the Universe works come from a vast range of sources. Physics is the study of the universal behavior of matter and energy, so useful information can come from anywhere: from tabletop experiments in your local university’s laboratory to giant instruments buried deep in Antarctic ice, or huge radio telescopes like the one at the Arecibo Observatory in Puerto Rico.
Even the most famous examples of triumphant, elegant theory were responses to an experimental fact.
That said, if you want to study how particles behave, you can’t do much better than to smash them together to see what results. For that we need particle accelerators, and the higher the energy you can get those particles moving, the better. Today the most energetic particle collisions we can achieve are at the LHC, where we smash together protons that carry kinetic energy 6,500 times the rest energy of the proton. It is here that we discovered the Higgs boson, and it is here that the attention of particle physicists (both experimental and theoretical) is currently focused, as we await new results later this summer.
However, the LHC is not a do-anything machine. And the massive detectors that we use to measure the products of these particle collisions are not the see-anything sensors from Star Trek. These instruments were designed in light of the Standard Model and optimized for certain searches. When theorists think about LHC results, we must deal with the fine details of these technologies: how they work, what they can measure, and what they cannot do. Even simple questions like “How many protons did you collide today?” can only be answered through the hard work of many experimental physicists. I am a theorist, and I have spent the last few articles in this series explaining quantum field theory and the Standard Model, but now I will look closely at the experiments—how the LHC works and how the LHC detectors work—to give you an idea of not just what we can measure and how, but of the immense efforts by thousands of experimental scientists over decades. This is the work that allows us to tell deep stories about the Universe.
The Collider
The LHC is the world’s largest particle collider. It is also the most powerful, and those superlatives are not unrelated. The main ring of the LHC is a tunnel 27 kilometers in circumference, buried roughly 300 feet under Geneva, Switzerland, and extending into France. Inside this tunnel there is a sealed enclosure, about 6 centimeters across, which is kept at a vacuum similar to that of deep space (10 percent of the moon's atmospheric pressure). Inside this near vacuum, protons are circulated in two beam pipes. Each beam travels at 99.999999 percent of the speed of light, one clockwise, one counterclockwise.
At such speeds, it is far more convenient to speak about energy than to speak about speed, so we say that the LHC can accelerate protons until they have 6500 GeV (giga-electronvolts) of kinetic energy. For comparison, the energy equivalent of the mass of a proton (by E = mc2) is slightly less than 1 GeV. The heaviest known particle, the top quark, has a mass of 175 GeV. The point of the LHC is to make the two counter-rotating beams of high-energy protons cross at specific collision points so we can see what happens when two protons with that much energy hit each other.
With those high-energy targets in mind, the design and immense size of the LHC ring is driven by basic physics considerations.
First, the LHC is a circular collider capable of returning the particles to be smashed to the collision point over and over, rather than a linear accelerator that allows for only one “crossing” of the beams, because it takes a lot of energy to accelerate protons up to 6500 GeV. When beams of protons are brought together to collide, virtually all the protons “miss” each other, traveling straight through the collision points. If the LHC were a straight line, these unused protons would be lost. Instead, the LHC’s rings bend the unused protons around for a second (and third, and fourth, and fiftieth, and millionth) pass. At those speeds, the next chance comes fast: the accelerated protons take one ten-thousandth of a second to travel 27 kilometers.
Now things do not naturally travel in circles; to keep any object moving on a circle requires a force. The faster the object is moving (the larger the kinetic energy), the greater the force you need. The smaller the circle, the larger the force as well. The force that keeps the protons at the LHC on their circular racetrack comes from a magnetic field created by powerful superconducting magnets. These line the entire 27 kilometer beam pipes, pulling the protons around on their circular orbit. These magnets are capable of generating a magnetic field of 7.7 tesla, more than 100,000 times stronger than the Earth’s magnetic field. (Regular medical MRI machines work with fields up to 3 tesla.)
The LHC needs 1232 of these “dipole” magnets, each 14.3 meters long. (There are roughly 8000 additional magnets that work to keep the beam of protons “focused,” with all the protons traveling in the same direction.) At the time of the LHC construction, these magnets were the optimal balance between cost, manufacturability, and magnetic field strength. (Also, their length was limited by the fact that they needed to be delivered to CERN on rural roads.) As a result, given the length of the LHC tunnel, 6500 GeV of energy is all that can be imparted to the protons. If the energies were higher, the magnets would not be strong enough to bend the protons enough to keep them on the ring.
If you look at the first runs of the LHC, the protons were given first 3500 GeV of energy, then 4000 GeV—far less than the 6500 GeV currently achieved. The Higgs boson was discovered in these “low energy” runs. The LHC was running at such a low energy—though still four times higher than any previous accelerator—because of problems with the magnets: it was too risky to operate them at the high fields that would be needed for higher proton energies.
To understand the risks, you need to bear in mind that the LHC magnets are not permanent magnets (like the magnets on your fridge). Instead, they work only when an electrical current is run through them. Running a current through a wire normally heats the wire, as the wire resists the flow of electrons. To minimize resistance, the LHC magnets are made from superconducting materials, which can carry electrical current without any resistance. However, superconductors need to be cold to work, and the superconductors in the LHC magnets—made of a niobium-titanium alloy—must be very, very cold: only 1.9 degrees Celsius above absolute zero (colder than intergalactic space). Cooling these magnets is a massive engineering problem. It requires an incredible refrigeration system, using vast amounts of liquid helium and a billion miles of niobium-titanium filament to make the superconducting cables. The magnet system is one of the major technical components of the entire LHC project—and the most expensive.
When you run a superconducting magnet at high field strength, you face a risk that the magnet might “quench,” meaning that some part of the superconductor might spontaneously become non-superconducting. The current then encounters resistance, which heats the rest of the magnet and makes the whole thing non-superconducting. If this happens, the magnetic field suddenly falls to zero. But a magnetic field contains energy, so the energy has to go somewhere. In the LHC, that energy ends up as heat in the liquid helium system, boiling it away.
Even simple questions like “How many protons did you collide today?” can only be answered through the hard work of many experimental physicists.
Turning liquid to gas in an enclosed area raises the pressure there: this is how steam engines work. The LHC was designed to safely shunt this pressure away in case of inevitable quenches. But in September 2008, just a week after the LHC’s opening celebrations, a magnetic quench occurred due to a faulty weld. The result was an electric arc that punctured a helium enclosure, followed by an uncontrolled release of boiling helium that overcame the safety mechanisms.
The pressure wave ripped some of the thirty-five ton magnets off their mountings, severely damaging fifty-three magnets, which needed to be repaired or replaced. It took fourteen months to repair the LHC, and—to prevent another incident until the safety mechanisms could be improved—it was decided to operate the magnets at lower field strength, reducing the risks of catastrophic quenches. For this reason, the data collected in 2011 and 2012 leading to the Higgs discovery was of protons traveling with 3500–4000 GeV of energy. After the discovery of the Higgs, the LHC was shut down for two years while all the interconnections were checked and improved, and the systems to shunt away helium gas safely were upgraded. However, even today, safety concerns limit the LHC protons to “only” 6500 GeV of energy, where the original design called for 7000 GeV. To get to that energy safely, the magnets will need further upgrades.
So the powerful magnets of the LHC keep the protons moving in a circle in order to bend them around multiple times to allow for the possibility of a collision with the counter-rotating beam. But how do you give protons such colossal kinetic energies in the first place?
The journey of the LHC protons starts from a small, commercially available bottle of hydrogen gas. Hydrogen is made of a proton and an electron, and the electron can be stripped away using an electric field, leaving protons behind. When the LHC is operating, it is “filled” with protons from the bottle. The protons are not spread smoothly out over the entire ring of the LHC; rather each “fill” consists of “bunches” of protons (2808 bunches in total), with each bunch containing one hundred billion protons. This sounds like a lot, but there are a lot of protons in ordinary matter: a single bottle of gas is sufficient to supply the LHC with all the protons it needs for four billion years of continuous operation.
From the bottle of hydrogen gas, the protons must gain kinetic energy. This is done using a number of smaller accelerators, each optimized to take protons at some low energy and boost them to a higher energy, before feeding them to the next accelerator. The full chain of accelerators goes from LINAC 2 (raising the protons up to 0.05 GeV), to the Proton Synchrotron Booster (up to 1.4 GeV), the Proton Synchrotron (26 GeV), the Super Proton Synchrotron (450 GeV), until finally the LHC ring itself. Several of these components were, in previous generations, cutting-edge accelerators. The W and Z bosons were discovered in 1983 in the Super Proton Synchrotron, for example.
Each stage of the acceleration chain uses radio-frequency (RF) cavities. To accelerate a charged particle, you need to apply an electric field, which pushes a positive charge in the direction of the field. RF cavities are metal boxes that have an electromagnetic wave sloshing back and forth inside. These waves are carefully timed so that, when the beam of protons enters one side of the box, the electric field in the electromagnetic wave at that location is pointed in the correct direction to speed up the protons rather than slowing them down. As the protons move through the cavity, the wave moves along with them, continuing to accelerate the charges. In essence, the protons “surf” the electromagnetic wave, gaining energy as they go.
By using a circular collider, protons can be brought through the same RF cavities many times, gaining energy each time. (Along the way, the beam of protons will be sliced up into the distinct bunches of protons for the LHC itself.) This is the second reason the LHC is a ring: in a linear accelerator each RF cavity would get only one chance to speed the protons up.
As the protons accelerate, the timing in the RF cavities’ electromagnetic waves must be adjusted so that each time the protons enter, the wave is correctly timed to push the protons faster. It is difficult and expensive to build a single accelerator that works well to accelerate protons from zero energy up to 6500 GeV; that is why the LHC uses a chain of accelerators that take protons at one energy, raise them to another, and then hand them off to the next accelerator. (This approach is also much more cost effective since the less powerful accelerators in the chain had already been built.)
Once the two beams of LHC protons have reached 6500 GeV, the RF cavities still have work to do. That is because circulating protons radiate away energy, which needs to be counteracted with the RF cavities in the main LHC ring. But the magnitude of the energy loss is smaller with protons than with electrons or positrons, and this is why the LHC collides protons. The downside is that protons are not great options for precision particle physics. As I wrote two articles back, a proton is a combination of many fields, all moving together: the gluons, the up quarks, the down quarks, the strange quarks, and so on. As a result, when you collide two protons, you don’t know what bits hit what, or with what energy. So we have to work very hard to overcome this lack of knowledge. Analyzing the results would be much easier if we could collide fundamental particles—excitations of a single quantum field—for in those cases we’d know exactly what was hitting what at every collision. The obvious choice would be colliding electrons, or colliding electrons with positrons, their antimatter counterparts. The problem is that the energy loss with electrons (and positrons) is vastly greater than the loss with protons—10 trillion times larger, in fact. We could not build enough RF cavities to keep up with that loss, or pay for the electricity bill to run them. Moreover, we’d have to deal with the massive bath of photon radiation coming off the electron beam, damaging the delicate superconducting magnets nearby.
The Experiments
We finally have our circulating beams of protons, separated into “bunches,” racing through their tunnel close to the speed of light, surfing on electromagnetic waves, their paths bent by superconducting magnets. What are we going to do with them?
Smack them directly into each other. At specific points around the LHC ring, additional superconducting magnets are used to squeeze the proton beams into a very small area, about 64 microns across (the width of a human hair). The two beams are also bent slightly inward, crossing at “interaction points.” At each interaction point, roughly 10–20 pairs of protons (out of the 100 billion in each beam) will hit each other, striking with something between a head-on collision and a glancing blow.
The LHC detectors are designed to image these collisions, see what they produce, and pick out interesting physics for experimentalists and theorists to puzzle over and understand. These detectors are tools and, like any tool, they are designed to do a particular job as best they can, given the limitations of the laws of physics. To understand that job and those limitations, let’s think for a moment about what the collision of two protons looks like, and what job we need a detector to do.
Since protons are not fundamental particles, when two of them hit, you cannot predict which two of the many fields that make up each particle are going to interact. It might be a gluon from one proton smashing into a gluon from the other, or a gluon and a up quark, or an up quark hitting an anti-strange, and so on. Each interaction candidate is called a parton, and each parton contains some fraction of the total 6500 GeV of energy that has been laboriously poured into the proton. We call the collision of the two partons the hard event (hard because it involves a great deal of energy), and we’ll return to it shortly.
Before we do that, let’s think about what happens to the rest of the protons, the fields that aren’t involved in the hard event. If it is rare for two protons to collide head-on, it is doubly rare for two pairs of partons two smash into each other. So if there is a collision, the rest of the two protons’ fields are not going to significantly interact with each other. But if you remove one parton from a proton (say, by slamming into another proton’s parton), the orderly motion of the conglomeration of fields that we identify as a “proton” goes out the window. The fields have to rearrange themselves, moving energy between the quarks, the antiquarks, and the gluons, to find new ways to oscillate in adherence to the rules of the strong nuclear force.
What this looks like is a massive shower of strongly interacting particles: the parts of the proton that are not involved in the hard event dissolve in an explosion of new particles. The originating protons were moving in a straight line through the interaction point with a tremendous amount of momentum, so this shower of new particles tends to continue along those directions. Thus, every collision of protons at the LHC contains hundreds and thousands of particles traveling in opposite directions along the path of the proton beams, the shattered remnants of the colliding protons. This is called the underlying event. Fortunately, the hard event can result in particles moving “sideways,” perpendicularly away from the beam. Few particles from the underlying event end up moving in this direction, so we have some prayer of distinguishing the physics of the hard event from the underlying event.
The hard event is where we go looking for something new and interesting: maybe the colliding partons coupled to the Higgs field, so the hard event contains a Higgs boson. Or maybe the hard event created a pair of top quarks, or W bosons, or maybe something completely new and unexpected. However, when new and very massive particles are created, they tend to decay very rapidly into lighter, longer-lived particles. This means that all this interesting new physics stays very close to the collision point: a Higgs boson, for example, can travel only 10-14 meters (about the radius of an atomic nucleus) before decaying.
Of the known particles, only a few live long enough to travel any reasonable distance, distances over which we can build a detector that can see them. These particles are the photon, the electron and its antimatter counterpart the positron, the neutrinos, the muon and its antimatter counterpart (these are heavy partners of the electron), and a number of strongly interacting particles similar to the proton called hadrons. As particles that are both electrically neutral and not strongly interacting, the neutrinos are completely invisible to any detector we can reasonably imagine building with current technology. But all the other particles interact via the electromagnetic force or the strong nuclear force. This tells us what we need from a particle detector: we need something that can “see” photons, electrons, muons, and strongly interacting particles. By “see” I mean measure their energy and momentum, and tell each of these particles apart from one another. And then the detector has one last, very critical job: it has to communicate this information to the outside world, where it can be recorded and studied by physicists.
How do the experiments do all that? I’ll concentrate on one of the two multipurpose experiments at the LHC: the CMS detector. The other, ATLAS, has very similar capabilities but achieves these using slightly different technologies and techniques. For experimentalists and theorists, those differences can be important—there are some things CMS is better equipped to do than ATLAS, and vice versa—but overall the two experiments are very well matched in their ability to detect particles moving away from the collision point. There are two additional experiments recording LHC collisions: ALICE and LHCb. However, their goals—and therefore their designs—are somewhat different from ATLAS and CMS, so I will have to skip over them here.

Image courtesy of CERN
Here I’m showing a picture of the CMS detector before it was closed up. You can see the beam pipe threading the center of CMS, followed by layers and layers of detector components. The whole detector is roughly a cylinder, 15 meters tall, 21 meters long, and weighs 14,000 tonnes. The “C” in “CMS” stands for “Compact,” as ATLAS is even bigger (though it weighs somewhat less).
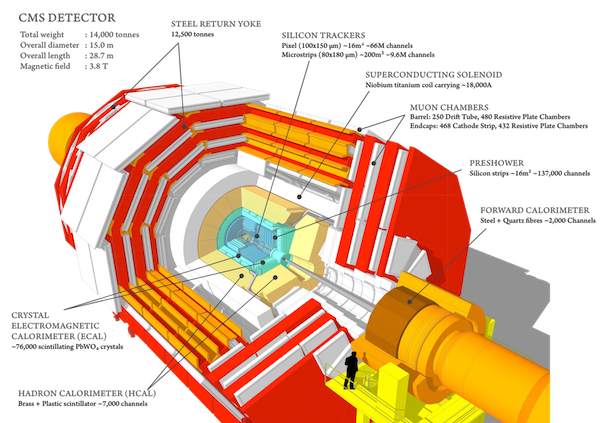
Image courtesy of CERN
The schematic above better illuminates the function of CMS than the photo. The beams cross at the center of the detector’s cylinder. The particles from the underlying event will generally go towards the flat ends of the cylinder, and the hard event will hopefully send particles into the “barrel” of the detector (though hard events can also send particles forward). Though we would love to have a detector that completely surrounds the interaction point, there have to be gaps for the beams of protons to enter and leave. So we can never see everything in the event; we will always miss the stuff close to the beam-line.
Before jumping to the center of the detector and working our way out, I’ll talk about the thing that makes CMS so heavy: a massive superconducting magnet capable of generating a 4 tesla field. To guide this magnetic field, the CMS detector contains an iron “return yoke.” It is all this iron that makes CMS so heavy.
Why does CMS need a massive magnetic field? The point of the detector is to identify particles, and doing so requires knowing their electric charge. Charged particles moving in a magnetic field, like the ones produced in the collisions, curve as they move: positively charged particles curve one way in the field (say, clockwise), while the negatively charged particles curve the other way (say, counterclockwise). Neutral particles will not curve at all. As the particles are moving very fast, a huge force needs to be applied if the curvature of their path through the detector is to be seen—thus the need for a huge magnet.
But how does CMS actually measure the curvature of charged particles? The first, inner layer of detector is the “tracker.” This is a finely segmented array of silicon pixels, similar in some respects to the CCDs (charge-coupled devices) used in digital cameras. The job of the silicon tracker is to record the path of every charged particle produced in the hard event. As a particle moves through the tracker and hits individual silicon pixels, those pixels record a small electric pulse, which is then conveyed out of the detector through wires. The pixels don’t stop the particles or rob them of much energy—just enough to record their presence. The pulses recorded by the silicon allow “tracks” of the particle motion to be constructed. CMS’s tracker is capable of recording particle position to within less than the width of a human hair. This requires so many pixels that the tracker alone has 75 million individual readout channels.
The tracker only records the direction of the charged particles’ motions, however; it doesn’t tell you what the particles are, or record their energy. For example, electrons and muons both have negative charge, thus both leave curved tracks in the same direction in the silicon. To distinguish them and other particles, CMS has two additional layers, called calorimeters.
The first calorimeter—the electromagnetic calorimeter—measures the energy of electrons and photons. The electromagnetic calorimeter is made up of blocks of transparent lead tungstenate crystals, 80,000 of them. As an electron, positron, or photon moves through these clear blocks of heavy metals, the interaction of the high-energy particle and the electrons and electric fields of the atoms in the crystals allows some of the kinetic energy to be converted into pairs of electrons and positrons, which in turn radiate off more photons and electron-photon pairs. The lead crystals need to be thick enough to contain most (if not all) of this shower of electromagnetic energy.
Once the particles in the shower have lost most of their energy, their passage through the crystal just excites the atomic electrons—giving them a little kick of energy, but not enough to create new pairs of particles. As the atomic electrons return to their original low-energy state, they scintillate, reradiating this energy out as photons—much lower-energy photons than the ones shooting out from the hard event. Photodetectors behind the calorimeter pick up this light; the more light there is, the more energy there must have been in the original particle that entered. This is why the crystals are transparent: to let the photon signal out to be seen by the photodetectors and recorded.
The electromagnetic calorimeter only measures the energy of the lightest particles, the electrons and photons, which produce copious amounts of lower energy photons and electron/positron pairs. Heavier particles don’t lose as much energy as they pass through the crystal, limiting the shower of radiation they leave behind to be seen in the scintillators. So if you see a track in the silicon pixels that points to a lot of energy in the electromagnetic calorimeter, you’re looking at either an electron or a positron, which can be distinguished by looking at how they curve in the magnetic field. Energy in the calorimeter without a pixel track must be a photon, because photons have no electric charge. We say the photon has a distinctive signature: no tracks in the inner detector, but energy in the first calorimeter layer.
Of course, this distinction is never 100 percent sharp: heavy particles can occasionally leave more energy than expected in the electromagnetic calorimeter, and electrons sometimes leave less than expected. One of the major tasks of the experimentalists is to calibrate their understanding of the detectors, quantifying not just what the expected result is, but what these outlier events might look like as well.
Of the known particles, only a few live long enough to travel distances over which we can detect them.
Tracks that don’t have energy in the electromagnetic calorimeter must be from either muons or hadrons. Hadrons are measured in the hadronic calorimeter, which works by interleaving sheets of brass and iron with plastic scintillators. When the heavy, strongly interacting hadrons smash into the metal, they shatter the nucleus and create a shower of particles. These pass into the scintillator, and—as with the electromagnetic calorimeter—create flashes of low-energy light that can be picked up by photodetectors and recorded. This process is less efficient than the mechanism in the electromagnetic calorimeter, requiring a lot of very dense metal to increase the probability that the hadrons smash into an atomic nucleus. Combining the energy recorded in the hadronic calorimeter with the tracks (and the lack of a signal from the electromagnetic calorimeter) allows identification of the hadronic particles.
The last layer of the detector is comprised of the muon chambers, out at the far edge of CMS. Not many particles get this far out from the interaction point: most have either spent their energy in the electromagnetic calorimeter or the hadronic calorimeter. In the Standard Model, only muons can elude both, leaving tracks in the silicon pixels (because they are negatively charged) but not in the calorimeters (or at least not much energy). Muons, or any other charged particle that somehow makes it out to the muon detector, hit a tube filled with gas: the charged particle ionizes the gas, ripping electrons from their atoms, which then drift to an electrically charged wire, imparting a small current. There are over two million of such drift tubes. That's the signature of a muon: curved path through the silicon in the same direction as an electron, no track in the calorimeters, then currents in the drift tubes.
This should give you an idea of the complexity of the systems needed to record the collisions at the LHC. And, remember, each element needed to be designed and built from scratch, then tested, installed, and calibrated. Every lead tungstenate crystal, for example, is slightly different from the others, and so responds to electrons and photons slightly differently. These differences must be characterized and understood by the experimentalists so they can correct for them.
Furthermore, the particle collisions give off damaging ionizing radiation; humans cannot safely approach any part of the LHC while it is running, or indeed for several days afterward. In fact, one way of measuring how many proton collisions have occurred at the LHC is just to measure the radiation levels inside the detectors. This bath of radiation slowly degrades the detector components, damaging silicon, clouding crystal, and so on. Experimentalists need to continually update their model of the detector to account for these sorts of effects.
To understand why it is essential for experimentalists to understand every aspect of the detector, consider not what we can see (electrons, hadrons, photons, and muons), but what we can’t see: neutrinos. We might want to know whether a proton-proton collision led to neutrinos (or some other invisible particle) being produced. But no element of the detector can see them, so how do we infer they were there?
The only way to do so is by adding up all the visible stuff and looking for where particles didn’t go. Conservation of momentum works for particles just as it does for macroscopic objects, so if you see an event where a lot of visible particles go this way, then something you didn’t see must go that way. But this only works if two conditions are satisfied. First, you must be sure that you can see everything going on in your detector; otherwise, the unbalanced momentum might be coming from a particle that avoided the detector elements by sheer happenstance. Second, it requires that you correctly measured the momentum of the particles you did see; otherwise, you might think the momentum is unbalanced because one or two detector elements measured too much or too little energy. Only ultra-accurate, up-to-date modeling of the detector can make this sort of measurement possible.
Getting the Message Out
In order to get enough proton-proton collisions to have a chance to see interesting new physics, the bunches of protons inside the LHC are separated by only 25 nanoseconds and travel very close to the speed of light. As a result, every 25 nanoseconds, a new collision occurs inside CMS. This means that 40 million collisions occur in each LHC detector every second. The full read-out from CMS or ATLAS—the response of every detector element during a collision—is about a megabyte of data. So if every event were recorded, CMS would have to write to storage 400 terabytes of data every second. Over a year of LHC operations, this would be 4000 exobytes of data. It is physically impossible for the LHC to record that much data. At most CMS and ATLAS can each record about 1000 events every second. You want to keep the interesting events, obviously—the events where you made a Higgs (for example), or something new and unexpected. So, somehow, the detectors need to decide which events to save, keeping only one event out of every 400,000.
Here is the problem. Light moves about 1 foot in a nanosecond, and no signal can move faster than light. So there is not enough time for signals about what happened inside CMS or ATLAS to leave the detector, go to a computer outside the detector, have that computer decide whether the event is “interesting,” and then send a message back to the detector saying “ok, this event was interesting, please save it.”
To deal with this problem, the detectors have to be capable of making decisions themselves. The calorimeters and the muon chamber have computing hardware built in, which is capable of assembling small pieces of the event and making a decision whether the event is likely to be interesting based on this partial information—maybe because there’s a muon in the muon chamber, or a lot of energy in one of the calorimeters which is unbalanced, indicating neutrinos or other invisible particles. From this first decision, some subset of the 40 million events can be sent along a little further away from the detector itself, for another level of decision-making with more information, until finally the lucky 1000 events per second are saved to long-term storage. This process of identifying and passing on an event that might have interesting physics is called triggering, and the hardware and software that does it is called the trigger.
Like the detector elements themselves, the trigger circuit boards built into the detector are bathed in ionizing radiation. Integrated circuits, like the ones in your cell phone, that are not radiation-hardened would quickly fail in this environment. Not to mention, the circuits are sitting in the middle of a 4 tesla magnetic field. If you’ve ever put a reasonably powerful permanent magnet next to your hard drive, you know how well computers and magnetic fields play with each other. Overcoming these problems were major design challenges.
Experimentalists have to decide what sort of events are likely to be interesting and design the trigger appropriately. The hardware can’t easily be changed if it turns out these decisions were wrong, so particle physicists spend a lot of time worrying about the trigger. How terrible it would be if the LHC were making all kinds of interesting physics but the trigger ignored these results!
The sort of events that the experimentalists want to trigger on are limited by what the detectors are capable of, but they are also motivated by the sort of things theorists have said are likely to be found at the LHC. Theorists like myself often lobby hard for expanding the criteria for what counts as interesting. However, there’s only so many things you can add, since every new addition that would let new events through must come at a cost of not recording some other type of interesting, trigger-able physics. We only can save 1000 events out of every 40 million, after all.
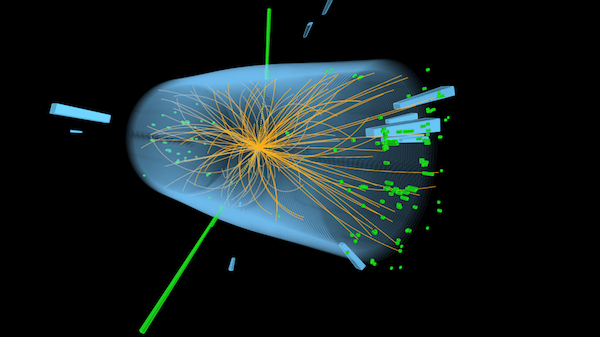
Image courtesy of CERN
The end result is a massive amount of data, recording events that look something like the above image. This is a real detector display from CMS, showing an event which was likely a Higgs boson produced in the first run of the LHC (2009–2013). The detector display has a sort of cartoon version of the detector. Green towers indicate energy deposited in the electromagnetic calorimeter, blue the hadronic. (Taller towers indicate more energy. This type of display is known as a LEGO plot, after the toy blocks.) Tracks in the silicon pixels are orange, and you can see them curving in the magnetic field. There are no muons in this event, so the muon chamber isn’t shown. You can see the massive profusion of particles close in to the collision point. Most of these aren’t interesting, just residue from the underlying event.
The most notable features of this event are the two giant green towers of energy in the electromagnetic calorimeter. These are not linked up to tracks in the pixel detector (there are no solid orange lines leading to the towers), so these are not electrons or positrons. That means they must be photons. This event was most likely triggered by the presence of these photons, as a pair of high-energy photons was known to be a likely place to look for new physics. Adding up the energy and momentum of these two photons would suggest that they came from a particle with mass of around 125 GeV. While it might be that these two particular photons did not come from a Higgs boson but rather other Standard Model processes, by collecting enough of these events, we can infer the existence of a new particle. This is what was announced on July 4, 2012.
Next time, I will tell the story of how that discovery was made—how collecting enough events like the two-photon event shown here can indicate new physics. As the one definitive discovery of a new particle in the recent history of accelerator physics, the story of the Higgs is a good case study for how future discoveries might proceed.
But through all of it, keep in mind the huge amount of work that the thousands of experimental physicists have put in to build and maintain the LHC and the detectors. It is easy for us theorists, sitting in our offices with nothing more than a blank piece of paper and a cup of coffee, to overlook their contributions, but without the experimentalists, the paper in front of me might as well remain blank.