Closing in on the Higgs

A 1997 simulation depicts the decay of a Higgs boson into four muons. Image couresty of CERN

Editors' Note: This is the sixth article in a series on the search for new physics at CERN.

In this series, I have:

1. Described the framework of quantum fields, the mathematical language we use to study fundamental particles and their interactions.
2. Sketched the Standard Model, including the Higgs field and the Higgs boson, which is the particle physics we understand.
3. Explained the operations of CERN’s Large Hadron Collider and the multi-purpose particle detectors ATLAS (A Toroidal Large Hadron Collider Apparatus) and CMS (Compact Muon Solenoid), which are the tools we use to study particles.

The series began, however, with some hints that something new might be lurking in the most recent data from CERN.

We still don’t know whether those hints will pan out. New data might reduce the statistical evidence of the possible signal to insignificance. On the other hand, the new data might strengthen the evidence for new physics. Still a third possibility is that the new data will be inconclusive, and we’ll need to remain patient. A conference in early August will present the latest findings, and when I know, I will let you know.

While we wait, I want to tell you more about the last time we discovered a particle: the Higgs boson. I’ve already talked about the Higgs field and the Higgs mechanism, which are central parts of the Standard Model. These ideas were understood theoretically as early as the 1960s, but the experimental quest for the associated particle took forty years. By understanding the history of false alarms and the final genuine discovery, we can gain insight into the current mix of uncertainty, caution, and excitement about the possibility of discovering new physics once again.

• • •

Three sets of theoretical physicists proposed the Higgs mechanism in 1964: François Englert and Robert Brout; Peter Higgs; and Gerry Guralnik, C. R. Hagen, and Tom Kibble. Papers by all three introduced the idea of a new field with a nonzero value everywhere in space-time, but Higgs’s paper was the only one that mentioned the particle associated with the field. As a result, the particle—though only hypothetical at the time—came to be called the Higgs boson.

The Higgs boson is a necessary consequence of the structure of the Standard Model. Because fermion fields—the quantum fields associated with matter—can be left- or right-handed, there must be some field that is always and everywhere in the background to “absorb” the difference between the two, a field that permits the left and right to be versions of a single matter field. That background field is required in order for fermions—matter particles like quarks and electrons—to be massive rather than massless.

The idea that the mass of a fermion comes from its interaction with a background field—that it is not simply given—leads to a definite prediction: that the excitation of the background field, which we call the Higgs boson, interacts most strongly with the more massive (heavier) fermions. If fermions have mass because they interact with the background field, then the magnitude of their mass is fixed by the strength of that interaction (the “coupling”).

This is how fermions work, but a similar idea applies to the other type of fundamental particle, the bosons. The Higgs field also interacts with specific combinations of the force-carrying gauge bosons associated with two of the fundamental forces of the Universe: the weak nuclear force and a force called hypercharge. Because of these interactions, the particles we know as the W and Z gauge bosons gain a mass. Again, this yields a specific prediction: since the W and Z particles gain their mass through interactions with the Higgs field, the Higgs boson must have large interactions with the W and Z. The other bosons that are part of the Standard Model, photons and color gluons, have zero mass because they do not couple with the Higgs field.

This prediction can be made extremely precise. Based on the measurements of the strengths of electric and weak nuclear forces, we can predict the W and Z masses. The agreement of the experimental measurements of these masses with the theoretical predictions lent a great deal of weight both to the general idea that there was a field with a nonzero value everywhere, and to specific ideas about the properties of this field.

In predicting the mass of the W and Z, the architects of the Standard Model also determined the precise nonzero value that the Higgs field sits at (its non-zero vacuum expectation value, which is 246 GeV). Therefore, long before we had any hint of the Higgs boson, we knew a great deal about the Higgs field.

What we did not know was the mass of the Higgs boson. It turns out that, just as the Higgs gives mass to the fermions and the W and Z bosons, it also gives mass to itself. Recall that what we call mass for a particle is the minimum amount of energy an excitation of a field needs in order for that excitation to be self-sustaining. Think of mass as a measure of the stiffness of a field, its resistance to oscillations when you try to make it move. Critically, the Higgs field interacts with itself: in the language of quantum field theory, the Higgs field is self-coupled.

When you give a self-coupled field a nonzero value everywhere in the Universe, you make it difficult for that field to oscillate. The greater the self-coupling, the more the field resists. Therefore, to know the mass of the Higgs boson, you need to know the strength of the self-coupling of the Higgs field. But herein is the problem: this self-coupling shows up nowhere else in the Standard Model, so no other measurement can tell us the mass of the Higgs boson. You need to find the Higgs itself.

The theorists of the 1960s and ’70s thus found themselves in a tricky situation. They had worked out the structure of the Standard Model, so they knew there must be a Higgs boson, but they had no idea how to go looking for it. It could be much lighter than a proton or much heavier. For any given mass, the exact properties of the Higgs could be calculated, but the mass itself could only be determined by producing the Higgs in a collider and measuring it. This might be the ultimate example of looking for a needle in a haystack—the vast haystack of all possible energy scales in the Universe.

But not all hope was lost, in part because theorists knew that the Higgs couldn’t be arbitrarily heavy.

In quantum field theory, if a self-coupling gets too large, the theory becomes strongly interacting. Quantum chromodynamics, for example—the theory of the strong nuclear force—is a strongly interacting theory. But as we saw earlier in this series, when fields are strongly interacting, calculations become mathematically intractable because one set of excitations in a quantum field is inextricably linked with every other excitation. If the Higgs boson were too heavy (above about 1200 GeV, 1200 times the mass of a proton), it would really be a composite particle made up of some other more fundamental fields. This wouldn’t mean that the Higgs mechanism was wrong, just that it would be incomplete, and we would have to develop a theory of the particles inside the Higgs, just as we have a theory about the quarks inside the proton.

Thus, if the Higgs really was just a single fundamental field, there was reason to pursue the idea that the particle would be light enough to detect with the energies achievable with a particle collider.

There was another reason for hope. In the Standard Model, we can calculate all sorts of particle interactions. One of these involves the interaction of two W bosons: we can calculate the probability that, if you threw two W bosons at each other, they would interact. It turns out that this probability grows as the energy of the two bosons increases. When the energy gets to around 2000 GeV (2 TeV), the probability goes above 100 percent.

Clearly, this is nonsense: you cannot have a process that occurs more than 100 percent of the time. What is missing is the Higgs boson. As the energy of the collision approaches and passes the mass of the Higgs boson, the Higgs itself enters the calculations for the interaction of two W bosons, keeping the probability to a (logically acceptable) number under 100 percent. Thus, the Higgs mass needs to be 2 TeV or less; or, if it is not, (for example if the Higgs is strongly coupled) something else must enter at or below 2 TeV to keep things sane.

So, going in to the Higgs search, we at least had some idea about upper limits on the Higgs mass. Whatever the Higgs mass was, we would find it below 2 TeV, or we would find something even weirder.

• • •

The first active searches for the Higgs boson were performed at CERN’s Large Electron-Positron (LEP) collider, which smashed electrons and positrons together using the same tunnel that was later reused for the LHC. Because electrons are so much lighter than protons, the LEP could reach energies only of about 200 GeV; the maximum ever reached was 209 GeV. By contrast, the latest runs at the LHC operate at 13,000 GeV.

While an electron-positron collider cannot reach energies as high as those a proton collider can, it does have the advantage that it smashes two fundamental particles rather than the conglomeration of fields that make up a proton. Thus, for every collision at LEP, experimentalists knew exactly which particles were colliding, and how much kinetic energy those two particles were carrying. Electron-positron colliders are therefore cleaner than a proton collider: to a first approximation, if LEP had enough energy to produce a new particle, the LEP detectors would be able to discover it. This is a far cry from the situation at the LHC, where interesting new physics could easily be hiding in the messy collisions of two strongly interacting composites, the protons.

So LEP could see any Higgs it creates; all of the LEP energy can be used to create new particle; and LEP had up to 209 GeV of energy. It stands to reason that LEP could search for Higgs bosons up to 209 GeV in mass, right?

Sadly, no. The strength of the Higgs interaction is proportional to the mass of the particles it interacts with. As a result, since electrons are low-mass fermions, they have a minuscule interaction with the Higgs field. So you cannot directly create any detectable number of Higgs bosons in the interaction “electron + positron = Higgs.”

Instead, LEP had to rely on the fact that Higgs bosons have large couplings to Z bosons, and Z bosons in turn have large couplings to electrons and positrons. So, the first thing LEP could do was create enormous numbers of Z bosons from electron-positron collisions and study their decays. If the Higgs were light enough, when Z bosons were produced, they would sometimes decay into a Higgs and a pair of matter fields (quarks, electrons, muons, taus, or neutrinos). This only works if the Higgs is significantly lighter than the Z boson (which has a mass of about 91 GeV). LEP looked for such decays and did not find them. The upshot of this null result? The Higgs mass had to be greater than about 58 GeV.

But if you can’t create the Higgs by itself because electron couplings are too small, and the Higgs isn’t light enough to be produced in the decay of a Z boson, what do you do?

Recall that the mass of a particle is the amount of energy you must put into a field to create a self-sustaining excitation. This means that a Z boson must always have energy and momentum that add up to the mass of a Z, which is 91 GeV. However, you can push energy into the Z field in a way that doesn’t add up to the Z mass, and still have the Z field oscillate, albeit briefly.

The field cannot sustain a long-lasting oscillation in this configuration. Very quickly the energy held in the Z field will be dumped into any other fields that the Z interacts with. When the excitation of a quantum field lacks sufficient energy and momentum to be stable over time, we say the excitation is a “virtual” particle. A virtual particle is an excitation of a quantum field, just like a “real” particle is an excitation of the field. But the virtual excitation doesn’t last for very long, while real particles are excitations that can last forever. Furthermore, virtual particles are rare; quantum fields would much prefer to create real excitations, if there is enough energy available.

Nonetheless, using virtual Zs was the best way for LEP to proceed. The experimentalists looked for the Higgs by trying to produce virtual Z bosons, which would then create a (real) excitation in the Higgs field and a real Z boson. That is, LEP tried to induce the reaction:

electron + positron → Virtual Zs → Higgs + Z

This would allow LEP to look for Higgses up to 118 GeV—the peak energy of 209 GeV minus the 91 GeV mass of the Z. If the Higgs were heavier, there wouldn’t be enough energy to create both a Higgs and Z at the end of the chain. (In fact the actual upper limit was about 114 GeV, slightly lower than this idealized maximum.)

Over the years, as LEP increased the energy of the colliding beams and collected more data, the Higgs search continued, eliminating heavier and heavier ranges. Combined with the theoretical upper limit theorists had worked out much earlier, this strategy was a glorified example of the process of elimination. As more and more masses were ruled out, the range of options that remained got narrower and narrower—heightening the anticipation of discovery. Then, right before LEP was to be shut down to allow the tunnel to be cleared and reused for the future LHC, a slight signal appeared.

This signal corresponded to a Higgs boson at around 115 GeV, right below the maximum possible Higgs mass that LEP could have found. But the data were not strongly statistically significant; there was more than a 10 percent chance that the extra events could have been the result of random statistical fluctuation alone. In terms of raw events, it was also not particularly impressive: the purported signal came from only about ten events among the four experiments, and of these ten, most of the statistical evidence was driven by only three events in a single detector (called ALEPH).

Nonetheless, the signal generated a great deal of discussion. We had expected to see the Higgs boson, but we didn’t know its mass. Here was a slight signal, the best we’d seen yet. The problem was that we didn’t have enough data. LEP was seeing events that looked like the decay products of a Higgs plus a Z boson, but only a handful, so the experimentalists’ ability to determine the origin of these events was limited.

The problem was that, even without a 115 GeV Higgs, the Standard Model could produce a similar set of particles that mimic this Z/Higgs pair—such events are called “background.” In the case of the three events driving most of the excitement, if there were no Higgs boson at 115 GeV, the LEP experiments should have expected to see around one of these background events.

Seeing three events when you expect to see one is suggestive of something new—a Higgs boson, in this case—since seeing such a large percentage increase is statistically unlikely. But with such small numbers, it is hard to be sure. Maybe there was no Higgs at 115 GeV, and LEP just got very unlucky and saw three events when they were “supposed” to only see one. It happens. (In this case, we expect it to happen about 10 percent of the time.)

The only way to know would be to collect more data. More data from a longer LEP run would reduce the chance of a random fluctuation producing the observed results—an elevated number of events over the background. Why? Because, all else being equal, as you increase the number of events producing a particular signal, the probability of a significant fluctuation from the expected result decreases proportionally by the square root of the number of events. Thus, more data means the relative error—what statisticians call the standard error of the mean—gets smaller, which means that large deviations from the expected value become far less likely. In particular, with more data it grows increasingly unlikely that LEP would see three times as many events as predicted (from the Standard Model background) without something new and interesting (like the Higgs boson) being present.

With enough data, it would be possible to reduce the chance of seeing the background randomly mimic the Higgs boson to 1 in 3,488,560, which is the magic number that we in particle physics have agreed constitutes evidence for discovery. This level of confidence is referred to as “5 sigma.” (The terminology is not as enigmatic as it sounds: the Greek letter sigma is used in statistics to denote the standard deviation of a set of data.) By contrast, the familiar “5 percent level of significance” from introductory statistics corresponds to a 2-sigma level of significance.

But it turns out that a longer LEP run was not carried out, even though it would have helped shed light on the anomalous signal, because continuing to run the LEP meant delaying the LHC. It takes many years to build an experiment as complicated as the LHC, and if the tantalizing hint of a 115 GeV Higgs was only a statistical blip, a great deal of time would have been wasted for nothing. In the end, the LEP was shut down in 2000, and for years theorists would talk of the 115 GeV Higgs that was (possibly) dangling right out of our reach.

• • •

The CERN directorate made the right call. There was no Higgs boson at 115 GeV, though we only knew for sure a decade later. The slight fluctuation turned out to be statistical noise: a few more events occurred than expected due to random chance, not because of a new particle. Statistically, this must happen. If you repeatedly toss a coin ten times, you would not expect to get five heads every time. Sometimes you might get six heads. Sometimes you might get three. And very rarely you might get ten heads, but it is possible. By contrast, if you got five heads every single time you flipped a coin ten times, you would rightly be suspicious. Deviations from the predicted average are a necessary part of random phenomena. But at the time of the LEP experiments we had no way of knowing that we were looking at a random fluctuation. No one made a mistake, and the data were fine; they were simply incomplete.

There is a lesson here, though a bitter one: sometimes statistical evidence for new physics—for a new particle—will evaporate with more data. You can do everything right, understand your detector and the background physics perfectly, and simply get “unlucky.” One might even say that there was never any evidence for new physics at all at this stage. Indeed the correct terminology for a deviation away from the background prediction is exactly that: there was some statistical fluctuation from a specific hypothesis, no more, no less. Of course, under this way of thinking, even a 5-sigma “discovery” is nothing more than a 5-sigma fluctuation from a background hypothesis. At some point, we must make a leap from these statistical statements to statements like “discovery” or “evidence.” There is no mathematical formula that can tell you when you should make these jumps. When it comes to 2- or 3-sigma fluctuations, there is a tension between experimental and theoretical physicists. The latter group—including myself—tends to be more eager to interpret the statistical deviation as meaning something.

As a field, we chose the 5-sigma level of statistical significance as the threshold that a discovery claim must meet in order to make the probability of mistaken discoveries very small, but this line is somewhat arbitrary, and that probability can never be eliminated. Experimental physics is not pure mathematics: there are no conclusive proofs, only sufficiently quantified uncertainties.

After the LEP was shut down and dismantled to make way for the LHC, the search for the Higgs moved to the only operational high-energy collider in the world at the time: the Tevatron collider at Fermilab, thirty miles west of Chicago. The Tevatron was a circular hadron collider like the LHC. Rather than accelerating pairs of protons, it smashed protons with their antimatter counterparts, antiprotons. Whereas the LHC can accelerate a proton to 6500 GeV of kinetic energy, the Tevatron could impart slightly less than 1000 GeV each to the protons and antiprotons, for a total energy of 1960 GeV in each collision.

In terms of energy, colliding protons with antiprotons has only slight advantages over colliding protons with protons (though it simplified the construction of the accelerator itself). That may be surprising, because we think of matter annihilating with antimatter as the ultimate release of energy—leveraging Einstein’s E = mc² to convert 100 percent of a particle’s mass into energy. But if the particles have been given thousands of times their rest energy in the form of kinetic energy, the extra kick from using antiprotons is pretty small.

Both protons and antiprotons are composite particles: they are made up of mostly of excitations of gluons as well as the lightest quarks (up and down quarks) and antiquarks (anti-up and anti-down). Like the electron, the very low mass of the lightest quarks means that the Higgs field doesn’t interact with them very strongly. Thus, producing a Higgs boson at the LHC is very similar to production at the Tevatron; it must proceed by indirect methods.

At both colliders, the Higgs could be made in one of two ways. First, high-energy protons (or antiprotons) can occasionally create pairs of W and Z bosons, which then interact to create a Higgs boson. This is not a common process, but it can happen.

The second method uses the fact that a proton is largely composed of fluctuations of the gluon field. Since gluons are massless, they don’t interact with the Higgs boson. However, they do interact with all the quarks. This includes the very heaviest quark, the top quark, which was discovered at the Tevatron in 1995. The top quark, by virtue of its enormous mass of 175 GeV, interacts very strongly with the Higgs.

Recall my description of coupled quantum fields as strings on a guitar, where plucking one string can cause the vibration to transfer over to the other coupled strings. In this case, the gluon strings are excited by the collision of a proton and an antiproton (or at LHC, of a proton and another proton). These oscillations can make their way over to the Higgs field, but only by first causing waves in the top quark field. The end result is that gluons—in a process called gluon fusion—can create Higgs bosons, but only indirectly.

These two production methods meant that the Tevatron could produce Higgs bosons. Of course, producing a particle is only part of the task: the Tevatron detectors also had to see the Higgs. Recall that the Higgs does not last very long, only 10^-22 seconds. So to detect the Higgs, we look for the particles it decays into. If the Higgs is heavy enough (greater than twice the mass of the W or Z boson), it will tend to decay into pairs of those gauge bosons. If it is heavier than twice the top quark mass, it will decay often into those heavy quarks. Such final states are what collider physicists find straightforward to look for: W and Z bosons can decay into electrons and muons, which are relatively easy to see. Top quarks too give spectacular signatures, due to the large mass (and energy) of the decaying top quark.

Lighter Higgs bosons—above the LEP limit of 115 GeV and under 168 GeV, which is twice the mass of the W boson—are somewhat more difficult to see. Such particles can decay into a “real” W or Z and a “virtual” W and Z, but this occurs less often than if the Higgs were heavy enough to decay into two real particles. Nearly every other decay of low-mass Higgs bosons (between 115 and 168 GeV) goes into pairs of gluons (via the interaction with the gluon field) or bottom quarks (the second heaviest fermion after the top quark). But these decays are a nightmare for detectors: bottom quarks and gluons are produced in enormous quantities in colliders through Standard Model interactions that don’t involve a Higgs, making it extremely difficult to tease a signal out of the data.

There is one more way the Higgs can decay, which is very rare—it happens to only 0.23 percent of Higgses—but very important. This is the decay of Higgs into a pair of photons. As with gluons, photons are massless and therefore don’t directly couple to the Higgs field, which is the source of mass in the Standard Model. However, top quarks have mass, so they couple with the Higgs field, and they are also electrically charged, so they couple with photons. Through the indirect interaction of Higgs to top quark to photon, the Higgs boson and photons can speak to each other, allowing for the Higgs to decay to photons. Moreover, while it is infrequent, this decay produces a very clean signature. If the momentum and energy of the two photons from a Higgs boson decay are summed up in the correct way, they will all add up to the mass of Higgs boson, creating a peak that sticks out over the background of Standard Model photons. The Standard Model predicts a bunch of two-photon (or diphoton) events, even without the Higgs. When you add the Higgs, you expect to see an increase in such events over the no-Higgs background.

• • •

What all this meant is that it was actually easier for the Tevatron to look for heavier Higgs bosons than lighter ones. Heavy Higgses would be produced at a lower rate because when you collide a proton and an antiproton, only a fraction of the energy is available to produce new particles (most of it is “wasted” in a shower of proton fragments). But they would produce easier-to-see final states, rich with electrons and muons from W and Z decays, which would be picked out over the omnipresent gluons and quarks that result from proton-antiproton collisions. Thus, by the end of its lifetime, the Tevatron could exclude a small range of Higgs masses at around twice the W mass. It could not, however, decisively rule in or out the hint of a 115 GeV Higgs from LEP.

The discovery of the Higgs would have to wait for the LHC, which had two major advantages over the Tevatron. The first was energy: though forced to collide protons at only 8000 GeV of energy (as opposed to the design energy of 14,000 GeV) due to problems with the connections between the superconducting magnets that surround the beam pipes, this was still four times more energy than the Tevatron could achieve. Higher energy meant high rates of Higgs boson production. The second advantage of the LHC was the vastly higher collision rate. The Tevatron, using antiprotons for one of the beams, was limited by the difficulty of creating antiprotons. The LHC just uses two proton beams, and protons are easy for us to get our hands on.

More collisions at higher energies meant more Higgs bosons could be produced. This meant that the LHC detectors could more easily see the decay products of the Higgs peaking over the background of similar-looking events that did not involve the Higgs.

The Higgs discovery was announced on July 4, 2012. But even before that, there were hints, some of which turned out to be misleading. In early 2011, both LHC detectors, ATLAS and CMS, saw some mild evidence for a Higgs boson at around 140 GeV. Each experiment had statistical evidence for something unusual going on which could be explained by a Higgs at this mass, at 2-sigma level of statistical evidence. This hint turned out to be a mirage.

By December 2011, new hints had taken center stage. (This is a common theme in particle physics: there is always a new anomalous result. Most of them turn out to be mere random fluctuations.) By combining every possible decay of the Higgs, both ATLAS and CMS could see evidence for a Higgs at around 125 GeV, now with over 3-sigma of evidence each. This evidence was largely driven by the Higgs decaying into pairs of photons.

At this point it was a game of statistics. The LHC needed to rack up enough proton collisions to create enough Higgs bosons, some small percentage of which would decay into pairs of photons. As this happened, the relative errors would decrease and a bump or peak of Higgs-induced photon pairs would appear over the background. You can see this happen in a nice GIF provided by the ATLAS experiment.

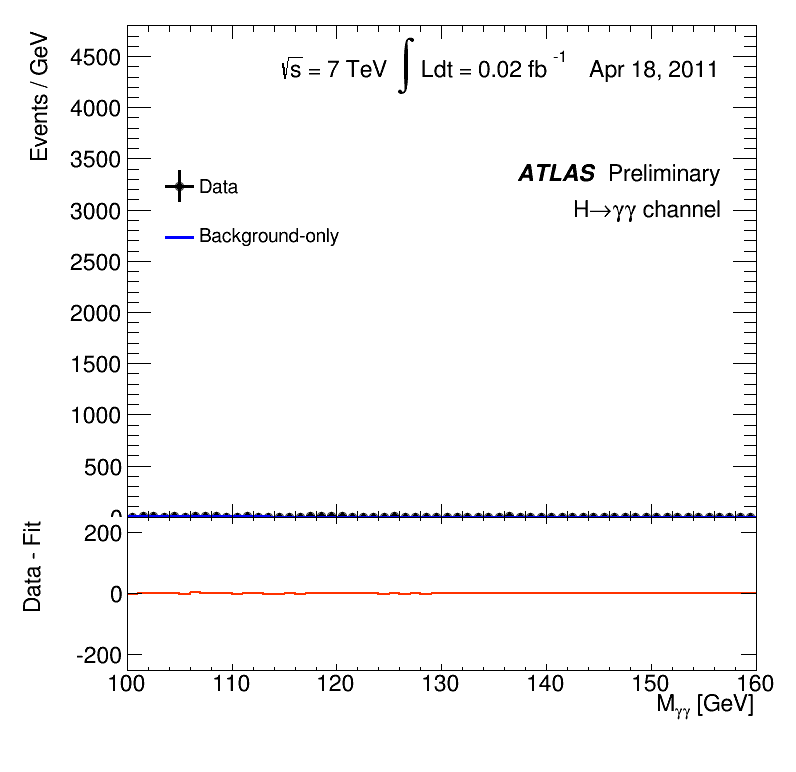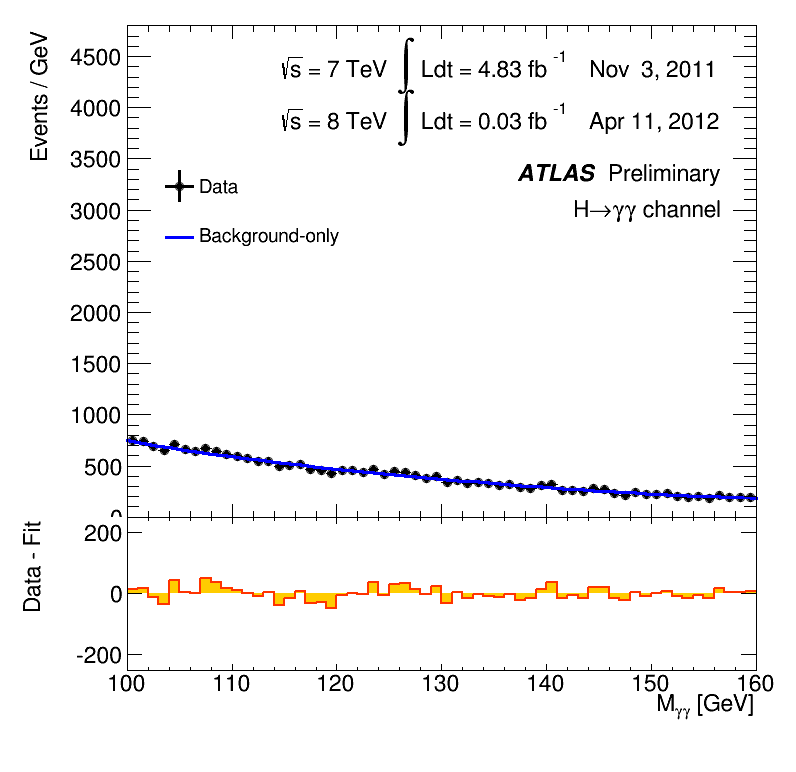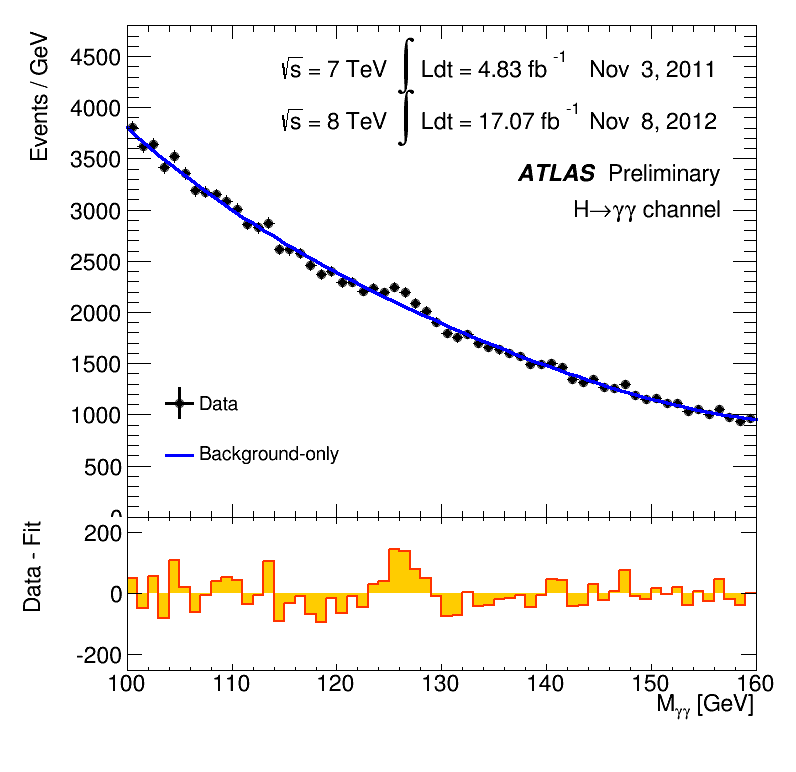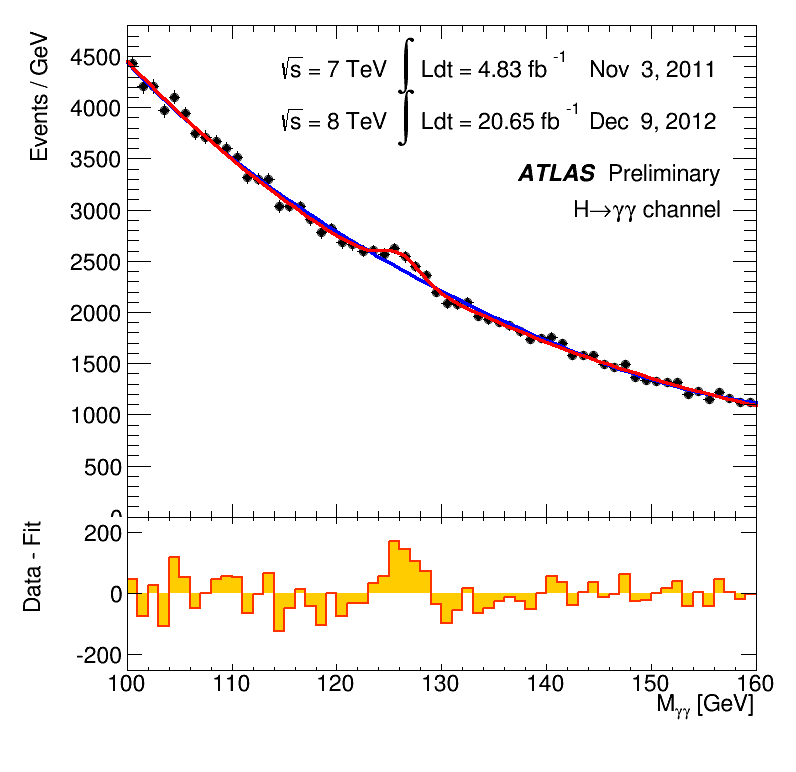
Image courtesy of CERN

This animation shows the “invariant mass” of the photon pairs on the horizontal axis. Photon pairs from Higgs decay have an invariant mass at the mass of the Higgs boson itself. As the animation runs, time passes and the data collected by ATLAS is added to the plot, and the number of photon pairs increases. In early June 2012, you can see by eye a small bump appear at 125 GeV. By December 2012 (after the discovery), the bump has grown, and it is blindingly clear that it cannot be any mere statistical error. This evidence was supplemented by additional decays of the Higgs into a real and a virtual Z boson, which then decayed into electrons or muons—another very clean, if very rare, signature of a Higgs boson.

At the July 4 announcement, both ATLAS and CMS individually combined searches for every way the Higgs could decay (the most important being photons and pairs of Z’s) to get enough statistical evidence so that both experiments, individually, could claim 5-sigma evidence for a Higgs boson at 125 GeV. Only once that bar had been cleared could the experimentalists confidently declare a discovery.

The reason for this caution should be clear: at least twice in the history of the Higgs search at colliders, evidence had accumulated for a Higgs boson at masses of 115 GeV and 140 GeV, where the Higgs turned out not to exist. The evidence was not clear-cut, but the odds of the signals being due to mere chance were small: smaller than 1 in a few hundred, if not a few thousand. That’s pretty good, good enough that most people would be willing to put money down at those odds.

But claiming the discovery of a new particle needs to be held to much higher standards. The 5-sigma threshold is an arbitrary line, but it has the advantage of being conservative, thus sparing us the embarrassment of a false discovery claim. In the modern era of particle physics, we have not yet had a particle “undiscovered.” We’d like to keep it that way.

• • •

Geneva is seven hours ahead of Chicago, where I lived in 2012. The day of the July 4 announcement I stayed up until 4 a.m. watching the conference at CERN. For weeks rumors had been swirling that this was going to be it, the announcement we had all been waiting for. A colleague and I had already begun working out some consequences of what we might be told. I frantically took notes as the ATLAS and CMS experimentalists revealed their results, and I spent the next day rushing to complete our paper.

I was not alone. Theoretical physics requires experimental data. We have spent forty years—longer than I have been alive, much less working in physics—thinking about the mysteries of the Higgs boson. Theorists far smarter than I am have developed very compelling ideas that might answer these riddles. But without data, we could not tell which of these clever ideas are right, if any of them are. The data announced on July 4, 2012, and in the years that have followed, have been incredibly important in beginning to answer these questions. We do not have the full story yet, which explains the excitement all particle physicists still feel about new results from the LHC, and why we theorists are so eager to think about surprising signals, like the one that kick-started this series.

In the next article, I will tell you about why we believe there is more particle physics out there, something or some things beyond the Higgs boson, waiting to be discovered at the LHC. These ideas might be wrong, but the problems they were invented to answer are very real.