Editors’ Note: This is the third piece in a series on the search for new physics at CERN.
CERN’s Large Hadron Collider (LHC) is located in a vast tunnel along the France-Switzerland border, 27 kilometers around and 300 feet underground. It was planned, designed, and constructed through a remarkable international effort, extending over a period of nearly twenty-five years at a cost of billions of dollars. Building it required great technical innovations and incredible collaboration by thousands of people. All with the promise of finding one thing: the particle known as the Higgs boson.
After 2000, the Higgs was the only missing piece of the Standard Model of particle physics—the theory that physicists developed in the 1970s to describe the properties of the most fundamental particles of the Universe and how they interact to make up the world as we experience it. As the structure of the Standard Model came into focus, physicists knew there had to be a new kind of quantum field, but less powerful particle accelerators, such as the Tevatron at Fermilab in Illinois and CERN’s own Large Electron-Positron Collider, had failed to detect it.
Even before the LHC was built, we physicists had very high confidence the new accelerator would be able to find it. But if the LHC had not found the Higgs boson, we still would have been incredibly excited. We would have understood that our grasp of nature’s basic components and their interactions was flawed. Contrary to some depictions in popular culture, scientists love to learn that our expectations are wrong. As Isaac Asimov once said, “The most exciting phrase to hear in science, the one that heralds new discoveries, is not ‘Eureka!’ but ‘That’s funny. . .’.”
Physicists also hoped that the LHC would discover things besides the Higgs. Perhaps the unusual signal I described in the first article of this series is just such a discovery; CERN is running more experiments as we speak and will give an update this summer. But unlike the search for the Higgs boson, latest efforts at the LHC include searches for phenomena beyond the Standard Model. We are striking out into uncharted territory, trying to find something that looks funny.
In the meantime, you should know about the physics we do understand. So my next two articles will describe the Standard Model, which unifies much of our basic understanding of nature. It is the basis for all of chemistry, as well as electricity, magnetism, and nuclear physics (including radioactive decay and nuclear fusion). In this piece, I will describe the fields and particles we know to exist, and how they interact, up to the part where the Higgs field gets involved. The rest of the story is for next time.
Physics, like all science, builds on previous work, so I must reference ideas I’ve already discussed. Most important is the notion of a quantum field, because the Standard Model is couched in the language of quantum field theory. Here are two key points to recall from my second piece. What we call particles—electrons, quarks, and photons, for example—are really wave-like excitations or oscillations of quantum fields. And if two quantum fields are coupled—as the quark field and the gluon field are—then excitations in one field can produce excitations in the other.
The Quantum Fields of the Standard Model
The basic ingredients of the Standard Model are easy to list, though understanding their properties is more difficult.
First there are the matter fields: three pairs of quark fields and three pairs of lepton fields. They are called “matter fields” because their particles form the stuff the visible Universe is made of.
Besides these fields, there are fields associated with the forces of Nature, which dictate how lumps of matter interact. These fields can be associated with classical “force fields” such as the electromagnetic field—though, unfortunately, they are nothing like Star Trek’s force fields that act like walls. But these are quantum fields, which means they can sustain wave-like oscillations that we call particles. There is a photon field for the electromagnetic force, a gluon field for the strong nuclear force, and the inelegantly named W and Z fields for the weak nuclear force. (Gravity, the fourth fundamental force of Nature, should have a quantum field and a related particle called a graviton, but the techniques of quantum field theory run into problems when applied to gravity, so this force is left out of the Standard Model. That is a whole other story.) Finally, there is one additional field, called the Higgs field, which is necessary for the whole edifice to hang together.
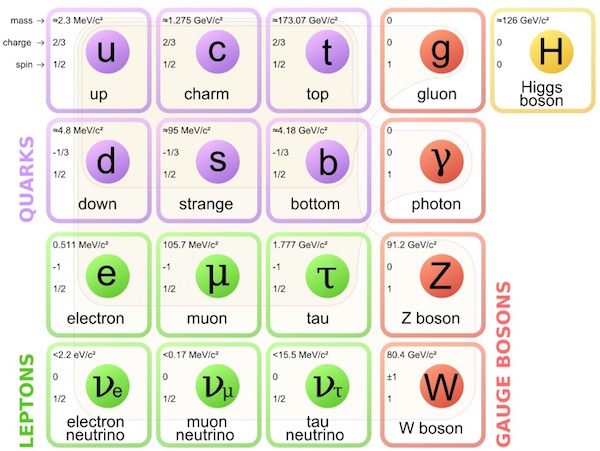
The particles of the Standard Model. Photo: Wikipedia
Three pairs of quark fields, three pairs of lepton fields, three interaction fields, plus the Higgs field: that’s it. But what distinguishes a quark from a lepton, or the matter fields from the fields associated with forces? To answer these questions I will look closely at each ingredient, but first I must explain the differences between matter and force, and between matter and antimatter.
Matter versus Force
One difference between quantum fields that correspond to matter and quantum fields that correspond to forces has to do with a very important property called spin.
Spin is related to angular momentum, the tendency of something that is rotating to keep rotating. For example, the Earth has angular momentum as it revolves around the Sun. This is an example of what particle physicists would call orbital angular momentum—the angular momentum of an object pivoting around some central point. Large composite bodies like the Earth are not the only things that can have orbital angular momentum. Particles can have this kind of angular momentum, too: the electrons in atoms, for example, which have orbital angular momentum around the central nucleus.
Besides orbital angular momentum, the Earth has another form of angular momentum due to the spin of the planet around the north-south axis. Puzzlingly, quantum particles can have a similar form of spinning angular momentum that is independent of any motion of the particle through space. We call this form of angular momentum the spin of the particle, in analogy with the spin of the Earth. I say this is puzzling because despite the name conjuring up the image of a particle spinning on an axis, quantum particles are infinitesimal points: they have no physical size, which in the non-quantum world is a prerequisite for having angular momentum from spinning around an axis. So do not read too much into the terminology; a quantum particle does not rotate the same way the Earth spins. Spin is just something that excitations of quantum fields have: it is an intrinsic property of each field.
The key point about spin is that it is quantized: particles can only have specific, discrete amounts of it. These possible amounts are zero spin, 1/2 unit of spin, 1 unit of spin, 3/2 units, and so on—any multiple of 1/2 is possible. (The unit of spin is a fundamental parameter of the Universe called Planck’s constant, denoted ℏ. It is an extremely small unit: a spinning CD has an angular momentum of approximately 1031—ten million trillion trillion—ℏ.)
A very important property of quantum fields is that if the excitation of a quantum field has spin 1/2, or 3/2, or so on—what is called “half-integer spin”—then two excitations of that field cannot exist in exactly the same state. (“State” here means having the same position and momentum, among other properties.) This is Pauli’s Exclusion Principle, named for the great physicist Wolfgang Pauli. In contrast, if the excitation of a field has spin 0, or 1, or 2 or so on—what is called “integer spin”—the resulting particles can exist in the same state. The formal, mathematical proof of these differences is called the spin-statistics theorem. I’ve wracked my brain trying to come up with an intuitive explanation of it, to no avail. You’ll have to take it as given, unfortunately.
Particles with half-integer spin are called fermions (after Enrico Fermi),while particles with integer spin are called bosons (after Satyendra Nath Bose). Since fermions can’t exist in the same state—cannot, among other things, be in the same place with the same momentum at the same time—they have to be physically separated; in contrast, bosons can pile on top of one another. So a pile of fermions can—in fact, must—form an extended object, while a pile of bosons can collapse down to a small region. Thus, matter is made of fermions.
The quark and lepton fields all have particles with spin 1/2. Electrons are a type of lepton, so they are among the fermions. Other examples of fermions are the up and down quarks that reside in the protons and neutrons that compose the nuclei of all atoms. All the matter you see and experience is made up of these three fermions.
By contrast, the photon, gluon, and W/Z fields all have spin-1 particles, so they are bosons. (More specifically, they are called “vector” bosons, where “vector” means spin 1.) Light is made of photons, so you see via bosons. The Higgs field is a spin-0 field, so its particle—the Higgs boson—is also, as the name tells us, a boson (though a “scalar” boson rather than a vector boson).
This is a lot to take in, so let’s take stock before moving forward:
- The world is made up of quantum fields, and particles are the excitations of quantum fields.
- The excitations of quantum fields have spin (intrinsic angular momentum).
- Some excitations have half-integer spin: these particles are called fermions.
- Some excitations have integer spin: these particles are called bosons.
- Fermions obey the Pauli Exclusion Principle, which means they cannot be in the same state (including the same place at the same time).
- Bosons do not obey the Pauli Exclusion Principle, which means they can be in the same state (including piling up in the same place).
- Leptons (including electrons) and quarks are fermions; photons, gluons, and W/Z particles are bosons, as is the Higgs boson.
Matter versus Antimatter
For a particle physicist, matter is spin-1/2 excitations of quantum fields. What about antimatter? Antimatter is the plot device of a great deal of science fiction, and its easy to understand why: it reacts violently to the stuff we are made out of, destroying both itself and regular matter when brought into contact. That’s a very compelling property, both scientifically and metaphorically.
Antimatter is not just science fiction. It is real; we can make minute quantities of it in particle accelerators, and infinitesimal amounts exist all around us, for very short times. Potassium, for example, can undergo radioactive decay and emit the antimatter version of electrons (called positrons, which get emitted in Positron Emitting Tomography, aka PET scans). Bananas are rich in potassium, so every time you eat a banana, you are ingesting something that will produce antimatter inside you. (Don’t worry; it’s mostly harmless. A measure of harmless amounts of radiation is the “banana equivalent dose.”)
How does antimatter fit into the story of quantum fields and their excitations?
Remember that particles are excitations of a quantum field. If you wiggle a quantum field (that’s what you do in an accelerator!), like setting up a wave on a surface of a lake, the quantum wave that forms is what we call a particle. Picturing that wave on a lake, you could imagine setting up a second wave on the water that would exactly cancel out the first. Antimatter is that second wave: it is an excitation of a quantum field that exactly cancels the particle excitation. Because the anti-particle is a wave in the same field as the “regular” particle, it has the same mass and the same spin.
If a particle-excitation runs into an anti-particle excitation, they cancel each other out, and the quantum field returns to its resting, unmoving state. Of course, both those waves had energy—that is what got the fields excited and moving in the first place. When they cancel each other out, the energy has to go somewhere: energy is always conserved. So it goes into the other fields that are coupled to the one that contains the particle-anti-particle collision. For the types of matter and antimatter we tend to have around, the coupled field can be the photon field: that is because the quarks and electrons, which make up matter, and the anti-quarks and positrons, which make up antimatter, all have electric charge, and photons couple with electric charge. So annihilating matter with antimatter creates a blast of very high-energy light (a powerful excitation of the photon field)—in other words, a giant explosion.
In truth, both types of excitations—matter as well as anti-matter—are “particles.” We only call one “matter” and the other “antimatter” because we live in a Universe where there’s more of the matter type of excitation and not much of the antimatter type. Why is that? This is one of the outstanding mysteries of particle physics. Something very early on in the history of the Universe selected one type of excitation over the other, and we don’t know how. We can hope that whatever lurks beyond the Standard Model—possibly discoverable at the LHC—might resolve this question.
Quarks and Gluons
Now that we’ve distinguished fermions from bosons and matter from antimatter, let’s look closely at each type of field of the Standard Model.
I’ll start with the quarks. Quarks come in six types, sometimes called flavor of quark, which are grouped in three pairs called generations. Pairing the generations together, the six types are called up and down (first generation), charm and strange (second generation), and top and bottom (third generation). The top is a heavier version of the charm, and the charm is a heavier version of the up. Likewise, the bottom is a heavier version of the strange, which in turn is a heavier version of the down. Each quark field has particle excitations (the quarks) and anti-particle excitations (the anti-quarks). The antimatter names are easy to guess: anti-up, anti-down, anti-strange, and so on. Most of what I will tell you about quarks applies to both the quarks and the antiquarks.
As far as we can tell, the only difference between the three pairs of quarks is their masses; each successive generation is more massive than the previous, ranging from a few thousandths of the mass of a proton for the up and down quarks to 175 times heavier than a proton for the top quark. There is no known pattern that explains the differences in the masses. (That is to say, knowing the mass of some of the quarks does not allow you to predict the masses of others.) We also have absolutely no idea why there are three nearly identical sets of quarks, though we know that there are only three generations. We do know that the heavier versions are unstable: if you excite a top quark field (say in a particle collider), the resulting particle will quickly disintegrate, transferring the energy in the excitation of the top quark field over to other particles, including lighter quarks. Thus, in everyday life, only the up and down quarks exist in any significant quantities.
Here is the subtle and really deep thing about quarks. When I said that there are six quark fields, that is actually a bit of a fudge. If I looked closely at any one of these fields, say the charm quark field, I would see that there are really three nearly identical fields. Each has almost exactly the same properties: they all are spin 1/2 and all have the same mass. Still, each has a slightly different value of some new property. Fancifully, this property is called color, for reasons that will soon become clear. So, to pick the charm quark as an example, you have three nearly identical charm fields, each with a different quantum color. You might call them the red charm, the blue charm, and the green charm. (The anti-charm would have anti-red, anti-blue, and anti-green options.) The natural thing is to try to figure out how these three different fields couple and interact with each other.
This is where things get very interesting. It turns out that there is no right way to designate the three charm quark fields as the red quark, the blue quark, and the green quark. We can tell that there are three distinct fields that make up the charm quark. Further, we can tell that how the three colored quarks interact with each other depends on which colors are involved: the way two red quarks interact is different than the way a red quark interacts with a blue quark. However, we don’t have a unique way to divvy these three fields up.
This is why the color analogy was chosen for quarks. Picture a color wheel. You know that once you pick three colors—“primary colors” as they are often called—you can build any other color out of combinations of those three. But which three colors should you start with as your basis of primary colors? The choice is arbitrary. Maybe today you pick red/green/blue, but maybe tomorrow you want to work with another set of three as your basis, say cyan/magenta/yellow. Those different sets of three colors are physically distinct from one another—they correspond to different wavelengths of light—yet in the end the result is the same: both choices allow you to paint with the full range of colors. Now, don’t take this analogy too literally; when painters or printers work with colors, the choice of primary colors generally is not arbitrary because there are practical concerns that make certain color bases more useful than others. The key point when it comes to quark color is that, in principle, it does not matter what three colors your start with. In a word, there is no distinguished basis.
It is in this respect that the quantum colors of quarks work like chromatic colors. We know there are three colors, and we can work with red, green, and blue if we want, but it turns out that we don’t have any reason to pick a single set of three quark colors as a canonical basis. If you sliced up these fields and recombined them—adding up bits of the red, green, and blue charms in different ways, resulting in what you might call the cyan charm quark, the magenta charm quark, and the yellow charm quark—and then worked out the interactions of these new colors, you would find exactly the same physical, measurable results as if you had stuck with your original combinations. This is why the color analogy is useful: it is like mixing red, green, and blue ink to get different colors. And it turns out the Universe has no particular preference for which sets of colors it paints quarks with.
This is a very powerful idea. It means there is a symmetry of Nature. A symmetry, in essence, is a distinction that makes no difference: you can make a change that has no impact on how a thing looks or works. When you rotate a circle around its center, for example, it always looks exactly the same. In the case of quarks, the laws of physics don’t care about the division of these three “colored” fields for each type of quark. If you change how you define the three fields, quarks still work in exactly the same way. This limits how quark fields can couple to each other, constraining the ways they can interact.
In fact, not only do the laws of physics not care if you choose red-green-blue or cyan-magenta-yellow—or any other set of three colors—as your basis of primary colors, they allow you to redefine the quark field colors in a different way at each point in space and time. This is an amazing and amazingly powerful feature of quantum fields. This type of symmetry is called a local gauge symmetry—“local” because you can make a different choice at every point in space and time. Demanding that the laws of physics work even if I continually redefine the three primary colors of a quark field places enormous constraints on how those fields can interact.
Forces Arise from Local Gauge Symmetries
Indeed, there is no way this could work if the three colored quarks fields were the only fields in the Universe. Imagine I start with a charm quark that I have called red at some particular point in space. Over time, this quark drifts to a new point in space, one where I have decided to redefine the quantum colors. That means I will view my red quark as a combination of these new colors: maybe it is now painted a nice magneta with yellow accents. But how quarks interact with each other depends on their colors, so this repainting matters. Yet the whole idea of a symmetry is that it should not matter.
The only way this can possibly work is if the quark fields are coupled to another set of fields, fields that also possess quantum color. Changing the basis of quark colors simultaneously changes the color basis associated with these new fields, and it does so in a precisely balanced way: these new fields exactly cancel whatever changes get introduced due to my redefinition of color. You might think of these additional fields as sort of a bookkeeper, tracking what color basis you choose at each point in space and time and then counterbalancing any changes in how quarks behave. In short, if I take the symmetry idea seriously—if I say, “quarks have something I will call color, which comes in sets of three, and the Universe requires local symmetry, requires that I be able to redefine color at each point without changing how quarks work”—then the rules of quantum field theory demand that there are more fields to prevent the changes in color bases from mattering.
But because this is quantum field theory, where there are fields, there must be particles too. What are the properties of these new particles? It turns out they must have spin 1—that is, they must be vector bosons. Also, they must have zero mass, they must couple with quarks, they must carry combinations of quantum color and anti-color, and there must be eight of them. All these properties are mathematical consequences of the application of quantum field theory to the particular gauge symmetry of quarks, with their three colors. The eight particles that fit the bill come from the gluon field.
Since the gluon field interacts with quarks, it can transmit forces between quarks. Again, picture a quark as an excitation in the quark fields. This excitation deforms the gluon fields around it. But an excitation in a gluon field is a particle—a gluon of some color—so we can describe this deformation as a quark emitting a gluon. Another quark wandering past will have its motion affected by this deformation in the gluon field; we can say that this other quark has absorbed the emitted gluon. Whenever there is a change of motion, we say there is a force. This force between quarks is the one we call the strong nuclear force. It works by gluon exchange: a quark (excitation in a quark field) emits a gluon (a deformation in the gluon field), and the gluon is absorbed by a second quark (a different excitation in a quark field).
At this point, you might say, “Wait a minute. You started this whole thing by saying that there was something called color, and that there was some symmetry in the Universe that lets me redefine color willy-nilly throughout space and time without changing physics. Then you told me that ‘oops, redefining color this way does change the physics, so I am going to add a bunch of new fields to cancel those changes out.’ Why bother? Why not just give up the requirement of local gauge symmetry, whatever that is anyway? Wouldn’t that make things simpler?”
One way to view these gluon fields and the resulting force—the view theoretical physicists like myself like to take—is that it is the necessary result of quarks having a particular, somewhat bizarre gauge symmetry. In a nutshell, the idea is that the Universe is enforcing this symmetry, and that this necessarily implies a force. Suppose you were to create a world with quarks that come in three colors and you decide that they should exhibit gauge symmetry: that you should be able to make different local changes everywhere without changing how things work. Then you must also create a bunch more particles (eight of them) that interact with the quarks, in a way that we would call “a force.” Without the force particles, the local changes in our definition of color would result in measurable changes in how the quarks move and interact. But we have demanded that there be no such changes: we wanted a symmetry, and a symmetry we shall have. Forces are local symmetries in action.
Experimentalists might take a different view. They might say: we know this force exists, we have measured it in the lab, and the symmetry story is one that was worked out afterwards, as theorists tried to come up with a mathematical model to explain the observations. To some degree, this is an accurate summary of how we developed the model of quarks and their color. Driven by experiment, theorists came up with this picture of a local symmetry, and then worked out consequences that were tested and confirmed by further experiments. In any case, all we can say is that quarks have this particular symmetry of their quantum color; we have no idea why they have this color or this symmetry (or why there are only three).
The Strong Coupling of Quarks and Gluons
Before moving on from quarks and gluons, there is one last complication to mention. In my last article I described how different fields can couple to each other. Theorists like myself are very happy when fields are weakly coupled—when excitations in one field only slightly affect the behavior of other fields. Strongly coupled fields are much harder to deal with; in some ways they are mathematically intractable.
As the name hints, the strong nuclear force involves a strongly coupled set of fields. Say you start with the blue down quark (though again, you could redefine this as a cyan-magenta down quark, or some other color combination). That blue quark, when moved, creates ripples in the gluon field. In other words, it creates, or emits, gluons. Emitting a gluon might change the blue quark to a red quark, the “blue-ness” leaving with the emitted gluon. So far, so good.
However, because of strong coupling, that emitted gluon will immediately cause excitations in the other quark fields: you will get excitations of red and green and blue quarks of the different generations, each also sending off more and more gluons. Rather than one field waving along happily, sending off nice discrete packets of energy in the form of a single gluon, the entire conglomeration becomes a roiling sea. Over short distances, each individual quark and gluon field can move somewhat independently, but from further away you cannot distinguish the individual fields: all the quark color fields and all the gluon fields are moving together.
Indeed, this strong interaction makes it impossible to separate quarks and gluons from each other completely. You cannot have a single, solitary red charm quark (or any other single colored quark). Only the full combination of three quantum colors is allowed. That is why we physicists adopted the “color” metaphor for quarks: you combine the quantum red/blue/green, and get a “colorless” combination, like combining red, green, and blue light to get white. Alternatively, you can form a colorless object by combining a quark and an anti-quark with opposite quantum color: red and anti-red, for example.
If you tried to pry the red quark, say, from its green and blue partners, the space between that red quark and the others would itself become full of excitations of the quark and gluon fields. This would act like a rubber band, pulling the wayward quark back, trying to reform a colorless combination. If you continued to force that quark away, you would need to put more and more energy into stretching that rubber band. Eventually, there would be enough energy in the band to create two new excitations of the quark field: one red and one anti-red. At this point, the rubber band of color would snap, sending the new red quark back toward the green and blue quarks (forming a colorless combination) and sending the anti-red anti-quark toward the original escaping red quark (again forming a colorless combination).
This need for quarks to form composite objects—called hadrons—is why we have particles like protons and neutrons. Each proton and neutron contains three quarks (two ups and a down for a proton, and two downs and a up for the neutron), with balancing quantum color. Inside the proton or neutron, the quark and gluon fields are a riot of activity, with quantum color being exchanged and excitations of the fields appearing and disappearing. So in addition to the three quarks, a proton or neutron also contains a multitude of gluons and additional excitations of all the quark fields (not just up and down, but charm, strange, top and bottom, as well as their antimatter components). These excitations, however, average out to just the three original quarks. I sometimes picture this as the quark and gluon fields all laminated together. Trying to wiggle just one field pulls the others with it; the proton and the neutron are just two ways that the laminated, stuck-together fields of quarks and gluons can move as a single unit. There are in fact a veritable zoo of hundreds of other such ways to wiggle the combined fields, all corresponding to what we would call a “particle.” However, each of these particles is made up, at their core, of some combination of quarks, antiquarks, and gluons, with a set of quantum colors that add up to “colorless.”
Zooming in to very short distances—less than about a femtometer, 10-15 meters—the strong nuclear force no longer appears infinitely strong: you can resolve the individual quark and gluon fields again. Continuing the analogy, you have gotten close enough to see the individual layers of our laminated field, and you can see the movement of one before it starts pulling the others with it. As the LHC slams protons together, the production of new particles like the Higgs boson must occur within this tiny distance, within the range where the individual colored fields can act independently of one another. As particles move outside of this range, the iron grip of the color force reasserts itself, and the quarks and gluons must rearrange themselves to form colorless combinations. So the LHC collides protons, but the real aim is to collide the quarks and gluons that make them up.
Leptons and Photons
After the complications of the quark and gluon fields, the lepton fields will be a little simpler. The word lepton means “light,” as in “not heavy.” At the time the word was coined, when quarks had yet to be discovered, the known leptons were all lighter than the particles made of quark combinations, like the proton and neutron.
Like quarks, leptons come in three generations. Each generation consists of a pair of particles: the electron and electron-neutrino (first generation), the muon and muon-neutrino (second generation), and the tau and tau-neutrino (third generation). Clearly the naming scheme for leptons is not nearly as whimsical as for quarks. Also, unlike the quarks, each lepton is a single quantum field—there are no hidden fields representing quantum color here.
Also like quarks, the lepton generations have increasing mass: the tau is heavier than the muon, which in turn is heavier than the electron. (The individual masses of neutrinos are not actually well known, but a full discussion of that would be a different set of articles.) Besides this variation in mass, each generation is identical to the previous, and again, there is no known reason for the existence of any of the generations beyond the first. Muons and taus are unstable and decay down to electrons, so the matter around you contains mostly electrons.
What makes each regular lepton different from its neutrino counterpart? The electron, muon, and tau have a very interesting property that the neutrinos lack: they have a symmetry. We saw above that the symmetry of quarks allows us to relabel quantum color everywhere without changing the laws of physics. For the electron, muon, and tau, you can redefine what is called the phase—when the peak and the troughs of the particle-excitations of the field occur—without changing the physics. Remember, a particle is really just a wave in a field, and a wave is something that goes from a maximum (a peak) to a minimum (a trough) and back again. This symmetry is a local symmetry: I can redefine when the peak of the electron field occurs differently at each point in space. Thus, this is another local gauge symmetry. The gauge symmetry in lepton fields lets us make separate changes of the phase of the wave functions at each point in space and time, without any change in how we see the particles move and interact.
This gauge symmetry is much simpler than the one for quarks that led to the eight gluon fields. It demands the existence of just a single new field. Again, you can think of this new field as what is required to cancel out all the changes in physically measurable results that would occur if you started relabeling the peaks of waves throughout space. We call this field the photon field. As before, the photon must be massless, it must be a boson with spin 1, and it must interact with anything that has this particular gauge symmetry.
Photons are the carriers of the electromagnetic force. Consider the repulsion of two electrons as they approach each other. An excitation in the electron field (say, one electron is moving toward another) generates an excitation in the photon field (emits a photon), which transmits to the other electron (absorbs a photon), which causes a deflection in its path. So electricity and magnetism—the very things that make all modern technology possible, as well as other nice properties such as holding the atoms in your body together and preventing you from falling through the floor—all of that is the result of fundamental particles not caring when their quantum waves peak. I find that rather strange and wonderful to think about.
To recap: the electron, muon, and tau have this symmetry, so they interact with the photon and have electric charge. By definition, we say the charge of the electron is -1. The muon and the tau have the same transformation under this symmetry, so they get the same charge: -1. Their antiparticle versions—the positron, the antimuon, and the antitau—have charge +1.
It turns out that the quarks also have this gauge symmetry, besides the one associated with color: they too are electrically charged because they operate similarly to charged leptons when you change the phase of their wave functions. The up, charm, and top all have charge +2/3, while the down, strange, and bottom are charge -1/3. (The antiquarks get the same size charge, but with the opposite sign.)
By contrast, neutrinos don’t care about this gauge symmetry, so they are electrically neutral. This makes them somewhat ghostly. Effectively every interaction you have with the world other than the downward pull of gravity is through the electromagnetic force: for example, picking up an object is using the electromagnetic fields generated by the quarks and electrons in your hand to nudge the quarks and electrons in the object in the direction you want the object to go. Chargeless neutrinos can ignore such prodding. As they are also without quantum color, they are immune as well to the strong nuclear force. Only the weak nuclear force affects them. I will discuss this force more in the next article, but as the name implies, it is a very negligible force indeed. Every second, a few trillion neutrinos pass through your body, and over your lifetime only a handful will ever bump into any particle in your body. (They will do no damage when they do, or at least, none compared to the myriad of more important natural sources of radiation all around us. They give far less than even 1 banana equivalent dose.)
Fortunately for us particle physicists, the electromagnetic force resulting from the gauge symmetry of charged particles is not a strongly coupled field theory. The interactions of a charge field and the photon field do not lead to massive feedback loops as with quarks and gluons. So we can calculate with high precision the behaviors of charged particles using the quantum field theory of photons, which is called quantum electrodynamics, or QED. By contrast, the quantum field theory account of color, called quantum chromodynamics or QCD, can only really be used in a simple way over the very small distances I described above, where you can resolve the different colored fields. It is somewhat amusing that the Universe has provided us with a starter-set for learning gauge symmetries: quantum electrodynamics works so nicely it allows us to get our mathematical bearings, as it were, before we strike out to the difficult strongly coupled quantum chromodynamics and the deeply confusing situation we find with the last force the Standard Model addresses: the weak nuclear force.
The W and Z bosons
Let us take stock. Remember the basic ingredients of the Standard Model: matter fields (associated with quarks and leptons), interaction fields (associated with gluons, photons, and W/Z bosons), and the Higgs field. We have now seen how quarks, leptons, photons, and gluons work, and how they are related to the strong nuclear force and the electromagnetic force. We saw, in particular, that the strong nuclear force and the electromagnetic force arise because of local gauge symmetries. The only fields that are left to explain are the W/Z fields and the Higgs field, and the only force left is the weak nuclear force.
I will delve into the oddities of this force next time, but here are the basics of the W/Z fields. The W and Z bosons are spin-1 particles. There are two W’s, one with electric charge +1, and one with electric charge -1 (they are antiparticle twins), while the Z is electrically neutral. All the fermions, both quarks and leptons, couple to the W and Z. Since the W’s are electrically charged, they can also interact with photons—after all, that is what electric charge means.
The W’s couple between pairs of quarks or leptons, linking the up quark field with the down quark field, for example, or the muon field with the muon neutrino field. A charge -1 muon can turn into an electrically neutral muon-neutrino either by emitting a W-minus or by absorbing a W-plus. A top quark (charge +2/3) can emit a W-plus and turn into a bottom quark (charge -1/3), or an anti-top (charge +2/3) could emit a W-minus and become an anti-bottom (charge +1/3). In each case, if you picture what is happening in terms of fields, the particle oscillation in one field (say, the top field) transfers its energy over to two other fields (say the W-plus and the bottom field), which we see as one particle decaying into two others. Notice that each of these pairs has a charge difference of exactly 1 unit. When changing from one type of particle to another, the unit of charge most go somewhere, and the W-plus or W-minus is where it goes. Emitting or absorbing W bosons is how you move between paired fermions in the Standard Model.
The Z boson, by contrast, has no charge. It acts somewhat like a photon: an up quark (or any other fermion) can emit or absorb a Z boson and remain an up quark. But unlike a photon, the Z is massive. This makes the force it creates very weak—thus the name weak nuclear force. Why is this?
Think of two electrons moving near each other. The electromagnetic force between them can be pictured as each electron causing disturbances in the photon field; these disturbances move between the two electrons, pushing and pulling on each. Two electrons moving near each other will also cause disturbances in the Z field.
However, the Z field has particles with a large mass; indeed the Z boson is about ninety times heavier than a proton. As I discussed in the previous article, the mass of a particle is a measure of how much energy an excitation of the field needs to be self-sustaining. (Remember that E=mc2.) Without sufficient energy, the oscillations die away quickly. Two electrons moving around each other have nowhere near enough energy to create a massive Z boson to throw between themselves. Any ripple in the Z fields created by the electrons dies away quickly, and the two electrons would need to be very close to each other for Z field to create a noticeable force between them. Because the W has a mass equivalent to 84 protons, it too creates only feeble forces over long distances. Thus, the weak nuclear force is weak because the associated particles are massive.
As you might have guessed, these W and Z fields are the consequence of a gauge symmetry, just as the gluon fields are the consequence of a color gauge symmetry and the photon field is a consequence of a phase gauge symmetry. You might even try to guess what that symmetry must be. Just as emitting or absorbing a gluon can turn a quark of one color into a quark of a different color, absorbing or emitting a W boson turns an up quark to a down or a charged lepton to a neutrino (or vice versa). So the symmetry would seem to have something to do with these pairs of fermions.
But you can also tell that something must have gone horribly wrong with the symmetry behind the weak force. When I talked about the strong force, I made a big deal about how the Universe does not care how you define color. You can redefine the colors at will and the physics works out the same. But you cannot do that with up quarks and down quarks, or taus and tau neutrinos: you cannot mix up the way you label them at will. In this case, the Universe very much cares about which fermion is which; we know this because they have different electric charges. So there is a contradiction: we have a symmetry (because all spin-1 bosons arise from symmetries), but not a symmetry (because we cannot arbitrarily label fermions the way we could arbitrarily label colors). To put it evocatively, the symmetry seems to be broken.
There is another way to see a contradiction here. The gluons and the photon are massless, while the W and Z have mass. But—and this is a very big deal—the rules of quantum field theory do not allow the force-carrying bosons to have mass. Again, this sounds like a simple contradiction: the weak force bosons have mass but they cannot have mass. Figuring out how this is possible is how Peter Higgs got a particle named after him. Next time I will explain how he resolved this apparent contradiction.